Vzorec modelu využívá cenu akcie, očekávané dividendy, realizační cenu opce, očekávané úrokové sazby, dobu do expirace opce a očekávanou volatilitu.
Co je Black-Scholes model?
Black-Scholes model je matematický model finančního trhu s deriváty. Termín Black a Scholes se vztahuje ke třem konceptům finanční matematiky. Rozlišujeme Black-Scholesův model, Black-Scholesovu parciální diferenciální rovnici a z ní odvozený Black-Scholesův vzorec. Tyto koncepty vypracovali v roce 1973 vědci Fischer Black a Myron Scholes.
Z parabolické parciální diferenciální rovnice v modelu, známé jako Black-Scholesova rovnice, lze odvodit Black-Scholesův vzorec, který lze použít k teoretickému odhadu ceny opcí evropského typu. Tento model také ukazuje, že opce má jedinečnou cenu danou rizikem daného cenného papíru a jeho očekávaným výnosem.
Výše zmínění lidé tedy vyvinuli vzorec, který lze použít k výpočtu ceny opce. Později tento model dále rozvinul Robert C. Merton. Proto se někdy označuje jako Black-Scholes-Mertonův model (BSM). Myron Scholes obdržel za jejich práci v roce 1997, kdy byl již Fisher Black po smrti, Nobelovu cenu za ekonomii.
Předpoklady Black-Scholes modelu
Black-Scholes model předpokládá, že trh se skládá alespoň z jednoho rizikového aktiva, obvykle akcie. Kromě toho se trh skládá také z jednoho bezrizikového aktiva, například hotovosti nebo státního dluhopisu.
Pro rizikové aktivum pak platí následující předpoklady:
- Aktivum vykazuje stochastický proces. To znamená, že musí splňovat požadavky teorie náhodného vývoje (geometrický Brownův pohyb (GBM)).
- U vybrané akcie se nevyplácí dividendy.
- Daný derivát je evropského typu, tj. existuje pouze jeden okamžik, kdy může dojít k realizaci (vypořádání).
U “bezrizikového” aktiva (hotovost nebo státní dluhopis) platí následující předpoklady:
- Peníze si lze půjčovat za stejnou průběžnou složenou úrokovou sazbu, která zůstává v čase konstantní.
- Můžeme nakupovat a prodávat akcie za libovolnou částku bez poplatků za obchodování.
- Trh nemá žádné arbitrážní možnosti.
Pomocí výše uvedeného modelu Black a Scholes ukázali, že je možné vytvořit zajištěnou pozici pro evropské kupní a prodejní opce. Toto zajištění se skládá z dlouhé akciové pozice a krátké opční pozice, jejíž hodnota nebude záviset na ceně akcií.
Jejich dynamická zajišťovací strategie vedla k parciální diferenciální rovnici, která určuje cenu opce. Z této rovnice je odvozen Black-Scholesův vzorec.
Oceňování opcí podle Black-Scholesova vzorce
Ceny opcí se určují podle Black-Scholesova vzorce, který využívá ceny akcií, realizační ceny opcí, čas, volatilitu a očekávané úrokové sazby. Přímo na trhu nelze sledovat pouze očekávanou volatilitu. Obvykle se odvozuje od ceny ostatních opcí. Níže si stručně vzorec vysvětlíme.
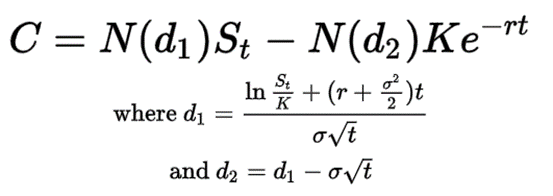
- C = kupní cena
- N = kumulativní distribuční funkce normálního rozdělení
- St = spotová cena aktiva
- K = realizační cena
- r = bezriziková úroková míra
- t = doba do vypršení platnosti
- σ = volatilita aktiva
Snadné vytváření kombinací opcí, rychlé zadávání příkazů nebo přehledný řetězec. Kvalitní platforma je základem pro úspěšné obchodování opcí. Tu pokročilou s nástroji jako OptionTrader či ComboTrader nabízí online broker LYNX. Objevte, co vše umí a jak dokáže zefektivnit trading.
V čem může Black-Scholes model pomoci opčním investorům?
Oceňování opcí je dnes řízeno elektronicky. Ceny opcí jsou stanoveny podle Black-Scholesova modelu. Chytré počítače neustále vypočítávají hodnotu opcí na základě několika proměnných. Díky tomu se obchodování s opcemi stalo transparentním a přístupným i pro soukromé investory.
Hlavní myšlenkou tohoto modelu je zajištění opcí nákupem a prodejem podkladového aktiva ve správném množství, čímž se eliminuje riziko. Tento typ zajištění se nazývá “průběžně revidované zajištění delty” a tvoří základ složitějších zajišťovacích strategií. Tyto strategie jsou velmi složité a obvykle je realizují velké investiční banky a hedgeové fondy.
Další použité zdroje:
BLEKEMOLEN, J. Black-Scholes model: formule voor de waardering van opties. LYNX [online]. Vydáno 21. 6. 2022 [cit. 30. 8. 2022]. Článek naleznete zde.